由于动量空间中能量弥散鞍点的存在，状态密度的范霍夫奇点一般存在于周期系统中。本文从高阶鞍点出发，引入了一种具有幂律发散态密度的二维范霍夫奇点。我们发现，在莫尔超晶格中，通常可以通过一个参数来调节能带结构来实现高阶范霍夫奇异性，例如通过调节扭转角或施加压力来调节双层石墨烯，通过施加垂直电场来调节三层石墨烯。并且讨论了在费米能级附近的高阶范霍夫奇点的相关效应。
 
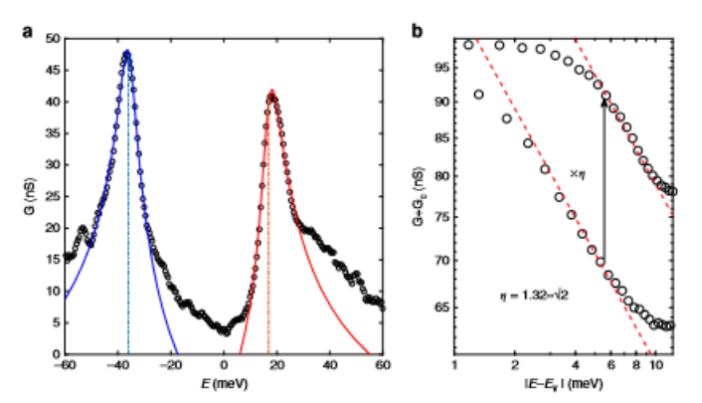
Fig. 1 理论拟合隧道电导测量。a空心圆是双层石墨烯在扭曲角为1.10°时的隧穿电导G，实线为拟合曲线。b E_v=16.72 meV处的峰以对数刻度绘制。
 
 
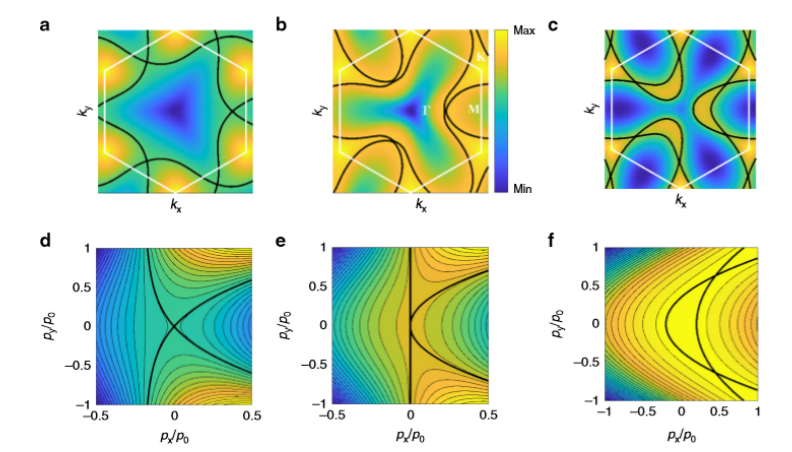
Fig. 2 范霍夫奇异点(VHS)拓扑转换期间的能量轮廓。a-c为能带结构计算的能量等值线，d-f为关于鞍点(3)的多项式展开。
 
 
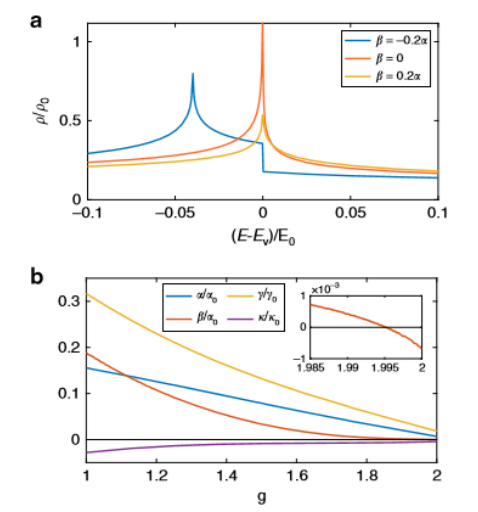
Fig. 3 VHS拓扑过渡过程中鞍点周围泰勒展开系数与态密度的关系。
 
 
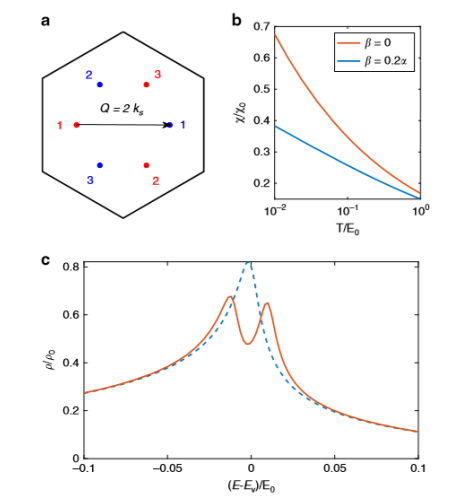
Fig. 4 双分子层石墨烯中的颗粒孔嵌套和密度波不稳定性。a MBZ中的六个高阶VHS，其中不同的颜色表示不同的波谷，而1，2，3各表示三个方向。b 谷间磁化率与温度的关系。c有(实线)和无(虚线)谷间密度波的状态密度。
 
      相关研究成果于2019年由麻省理工学院物理系Liang Fu课题组，发表在Nature Communications (https://doi.org/10.1038/s41467-019-13670-9)上。原文：Magic of high-order van Hove singularity