拓扑孤子是一类稳定的非线性激励，常在不同的领域中出现，如在核力的Skyrme模型中。在这里，作者认为类似的激发在通过堆叠和扭曲两层石墨烯获得的非凡材料中起着重要作用。接近魔角观察到的绝缘行为，将为掺杂的超导性提供路径。在这里，作者提出了对这两种观察结果的统一描述。对称性破坏凝聚态产生有序绝缘体，而凝聚态中的拓扑孤子——斯格明子——显示为带电荷的 2e 玻色子。通过计算，得到斯格明子的凝聚形成超导体的物理特性。作者展示了拓扑结构如何减轻库仑排斥并提供以前未探索的超导途径。该机制不仅阐明了为什么其他几种莫尔材料没有表现出超导性，而且还指出了预期具有强大超导性且未探索过的平台。
 
 
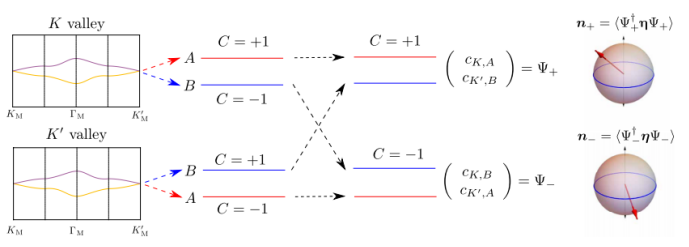
Fig. 1 定义赝自旋。
 
  
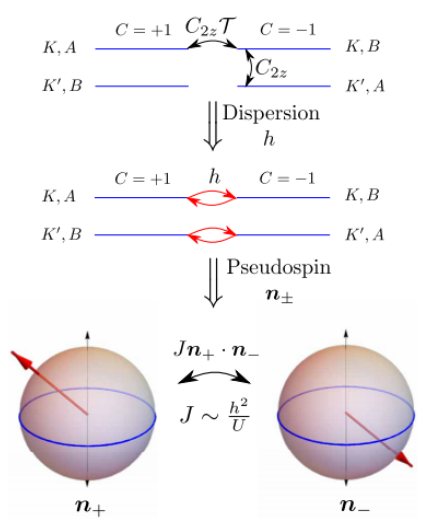
Fig. 2. 隧道诱导的超交换。
 
 
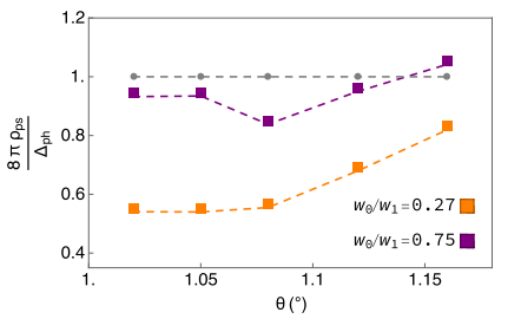
Fig. 3. 带电激发的能量学。
 
 
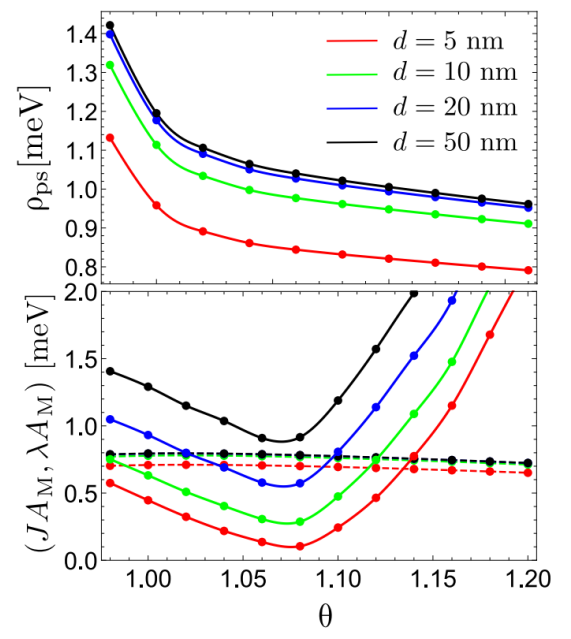
Fig. 4. Sigma 模型参数。
 
 
Fig. 5. 带电拓扑纹理的配对。
 
 
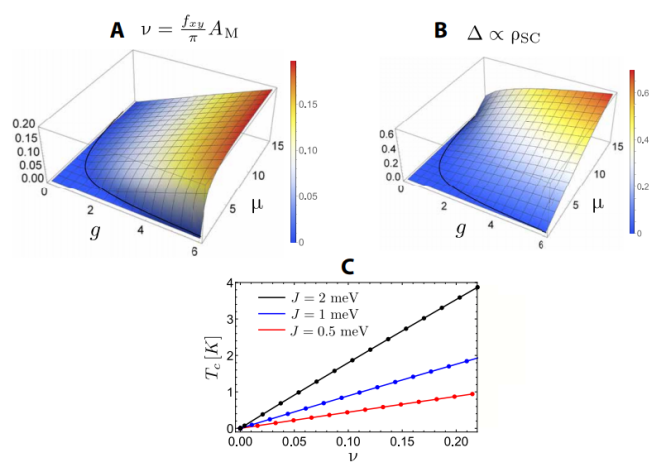
Fig. 6. 掺杂 CP1 模型的大 N 相图。
 
 
Fig. 7. MATBG 接近半填充v= 2。
 
        相关研究成果于2021年由哈佛大学Ashvin Vishwanath课题组，发表在Science Advances（http://advances.sciencemag.org/content/7/19/eabf5299）上。原文：Charged skyrmions and topological origin of superconductivity in magic-angle graphene。

转自《石墨烯杂志》公众号