研究描述了单层石墨烯的面外电介质极化率如何影响双层石墨烯的静电学Bernal (BLG) 和扭曲 (tBLG)。 研究使用密度泛函理论计算的极化率值与先前公布的 BLG 中静电控制层间不对称电位的实验数据和 tBLG 中的层上密度分布数据的输出进行比较。 结果表明，tBLG 中的单层通过极化率 α_exp= 10.8 ų 和有效的面外电介质磁化率 ϵ_z= 2.5 得到了很好的描述，包括它们在零磁场下的层上电子密度分布和在量化磁场时的层间朗道能级钉扎。
 
 
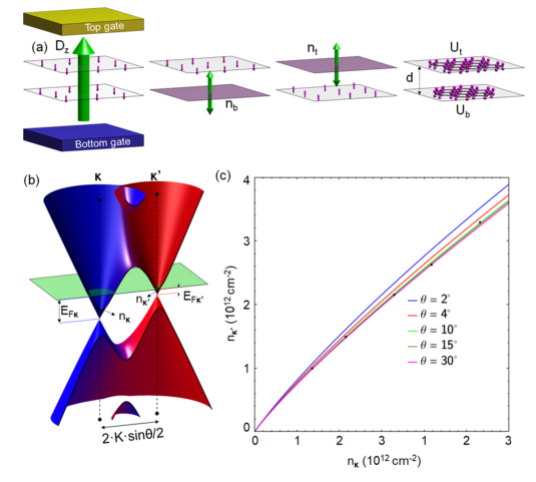
图1.  (a) 说明每个单层的介电极化率如何进入双层静电分析的草图。 (b) tBLG 中的特征电子色散（此处，θ = 3°；u = 100 meV）。 顶层/底层的电子态幅度用红色/蓝色表示。  (c) 单门 tBLG 中的微谷载流子密度 n_κ/κ' 为魔角范围外的各种错位角计算，与对应于SdHO的密度相比，在具有未知扭曲角的 tBLG 薄片中测量（黑点）。
 

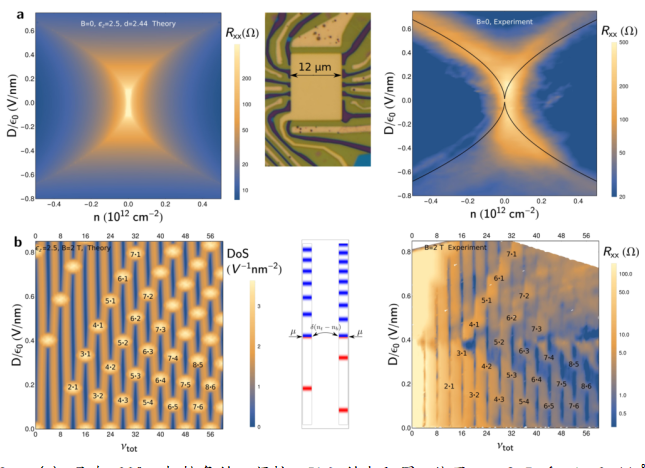
图 2.  (a) 具有 30° 扭转角的双门控 tBLG 的电阻图，使用 ϵ_z= 2.5 和 d = 3.44 Å（左）计算并测量（右）作为总载流子密度 n 的函数，和垂直位移场 D，在 B = 0 和 T = 2 K。 (b) 在 B = 2 T 的 30° tBLG 中计算的钉扎 LLs（左）和测得的电阻 ρxx（右）的状态密度 ，绘制为位移场和填充因子的函数。明亮的区域对应于标记的 N_t/N_bLL 钉扎条件。
 
  
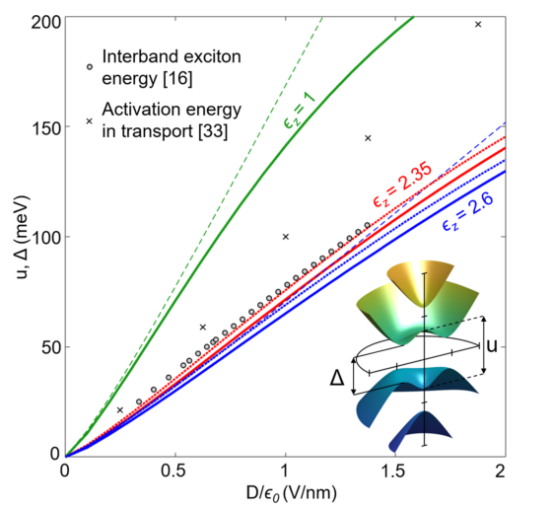
图 3. 未掺杂 BLG 中的层间不对称电位（虚线）和带隙（实线），使用不同的 ϵ_z= 1（绿色）、2.6（蓝色）和 2.35（红色）值自洽计算，并与参考文献中的传输间隙（圆圈）和光学间隙（十字）进行比较。 在这里，研究使用 v = 10.2·10⁶m/s，γ₁= 0.38 eV，v₃=1.23 ·10⁵m/s，v₄= 4.54·10⁴m/s，δ= 22 meV，d = 3.35 Å。虚线显示使用 γ₁= 0.35 eV 和相同的其他参数计算的间隙值。草图显示了四个 BLG 带（间隙下方 1,2 和间隙上方 3,4），突出显示了 u 和 Δ 之间的微小差异。
  
       相关科研成果由曼彻斯特大学Sergey Slizovskiy和Aitor Garica-Ruiz等人于2021年发表在Nano Letters（https://doi.org/10.1021/acs.nanolett.1c02211）上。原文：Out-of-Plane Dielectric Susceptibility of Graphene in Twistronic and Bernal Bilayers。

转自《石墨烯杂志》公众号