在本文中，我们提出了一个石墨烯在平面内变形下的完全非线性杆和弹簧模型。杆和弹簧的本构行为分别由修正的Morse势和非线性键角势定义。在考虑节点（原子）大位移的情况下，编写了代表性晶胞的平衡方程，并使用能量准则评估了解的稳定性。沿扶手椅和锯齿形方向的单轴载荷情况的解表明，石墨烯在小变形时是各向同性的，而在大变形时则表现出各向异性。此外，石墨烯在变形达到临界值后表现出负泊松比。在等双轴载荷的情况下，发现了多个平衡解，并且石墨烯可以经历不对称变形，尽管外部载荷是对称的。然后，通过引入小位移假设，将平衡的非线性公式线性化。推导了杨氏模量和泊松比的表达式。
 
 
图1. 石墨烯片被认为是一个杆-弹簧系统和通过在杆的中点放置虚拟原子而获得的代表性晶胞。
 
  
图2. 杆-弹簧模型元件的本构行为。(a)杆的轴向力和纵向拉伸之间的关系。(b)弹簧的弯矩和键角变化之间的关系。
 
 
图3. 石墨烯的代表性晶胞受到平面内大变形的分析。(a) 参考构型和变形构型。每种模态都有两个自由度，并引入约束以避免刚性运动。(b)由于键角变化而产生的在杆上的弯矩和剪力。
 
  
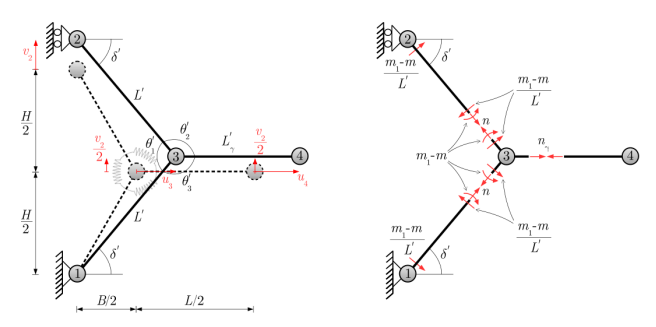
图4. 对称变形情况下石墨烯的代表性晶胞。(a)参考构型和变形构型。运动学简化了，现在只由三个自由度控制。(b)变形构型中的内部作用。
 
  
图5. 对代表性晶胞、扶手椅和锯齿形载荷情况进行了分析。(a)扶手椅形加载方向(x方向)。(b)锯齿形加载情况(y方向)。
 
  
图6. 定义影响长度用于计算作用在等效连续体上的应力。(a)扶手椅形加载方向。(b)锯齿形加载方向。
 
  图7. 扶手椅形和锯齿形单轴载荷作用下石墨烯的平衡路径。
 
 
图8. 单轴载荷下石墨烯代表性晶胞的运动学。(a)扶手椅形加载:节点位移。(b)锯齿形加载:节点位移。(c)扶手椅形加载:杆长变化。(d)锯齿形加载:杆长变化。(e)扶手椅形加载:键角变化。(f)锯齿形加载:键角变化。
 
  
图9. 等效连续体的弹性性质随变形的增加而变化。(a)切向拉伸刚度。(b)泊松比。
 
  
图10. 代表性晶胞的变形模式及其对等效连续体泊松比的相应影响。(a)扶手椅形加载方向。(b)锯齿形加载方向。
 
  
图11. 等双轴载荷作用下石墨烯的平衡路径。在极限构型（ε_lim，σ_lim）之前解是唯一的，在此之后，可以找到三个独立的解。(a)第一解。(b)第二解。(c)第三解。
 
  图12. 石墨烯代表性晶胞在等双轴载荷作用下的运动学。(a)节点位移。(b)杆的长度变化和本构关系表明在每种构型中，杆受到相同的轴向力。
 
  
图13. 石墨烯的稳定（实线）和不稳定（虚线）平衡路径。(a)扶手椅和锯齿形方向的单轴载荷。(b)等双轴荷载。

       相关研究成果由意大利“恩佐·法拉利”工程部、福州大学土木工程学院Matteo Pelliciari等于2021年发表在International Journal of Engineering Science (https://doi.org/10.1016/j.ijengsci.2021.103527)上。原文：A nonlinear molecular mechanics model for graphene subjected to large in-plane deformations。

转自《石墨烯研究》公众号