超导电性和相关绝缘体在magic-angle twisted双层石墨烯(MATBG)中的出现,提出了一种有趣的可能性,即其配对机制有别于传统超导体,正如Bardeen-Coopero-Schrieffer (BCS)理论所描述的那样,超导电性和相关绝缘体,在魔角双层双层石墨烯(MATBG)中的出现,提出了一种有趣的可能性,即其配对机制有别于传统超导体。然而,最近的研究表明,即使库仑相互作用被部分屏蔽,超导性仍然存在。这表明MATBG中的配对在本质上可能是传统的,是其平坦带的大的态密度(DOS)的结果。在这里,我们将隧道和Andreev反射光谱与扫描隧道显微镜(STM)相结合,在MATBG中观察非常规超导的几个关键实验特征。结果表明,在过渡温度T
c以下的隧穿谱与传统的s波超导体的隧穿谱不一致,而与具有各向异性配对机制的节点超导体的隧穿谱相似。我们观察隧道差距Δ
T之间存在很大差异,这远远超过了平均场BCS比率(2Δ
T / k
BT
c ~ 25),差距Δ
AR提取安德列夫反射光谱(2Δ
AR / k
BT
c ~ 6)。即使超导性被抑制,隧穿间隙仍然存在,这表明它是从伪间隙阶段出现的。此外,当MATBG与六方氮化硼(hBN)排列时,赝隙和超导性均不存在。这些发现和本文报道的其他观察结果为MATBG中超导的非BCS机制提供了优势证据。
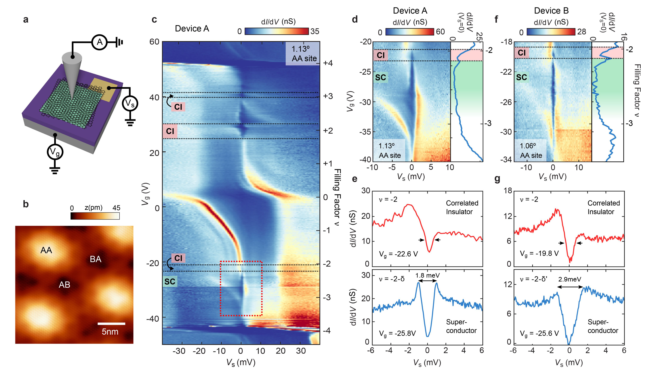
图1 超导MATBG隧穿间隙的扫描隧穿光谱研究 a,实验装置原理图。b, MATBG的STM地形图像。c,在A器件AA位点拍摄的Tunneling dI/dV(Vs, Vg)显示了固定在EF上的传导和价平带。d 器件A的高分辨率dI/dV(V
s, V
g)在ν =-2,和ν =-2与ν =-3之间的间隙。e 在Vg =-22.6 V和Vg =-25.8 V时,器件A的dI/dV(Vs)光谱。f,除B装置(1.06,0.1%应变)外,与d相同。g在V
g =-19.8 V和V
g = -25.6 V时,器件B的dI/dV(Vs)光谱。
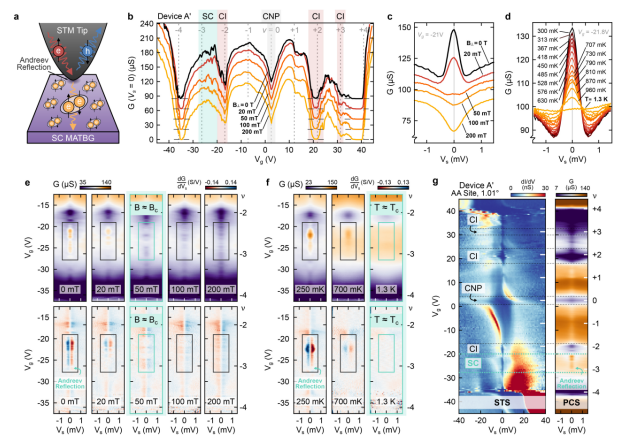
图2 MATBG的点接触光谱和Andreev反射 a利用密度调谐点接触光谱(DT-PCS)测量安德烈耶夫反射过程的原理图。b设备A在Vs = 0 V时接触点G(V
g)的切线c在0 T和200 mT之间的五种磁场强度下,在Vg = -21 V超导载流子密度范围内点接触G(Vs)谱线切割。d,线切的点接触型G (V
s)光谱, e在50 mT左右Andreev反射消失的面外磁场的不同值的点接触G(Vs, Vg)和dG/ dVs(Vs, Vg)。在1.3 K左右Andreev反射消失的不同温度值的点接触G(Vs, Vg)和dG/dVs(Vs, Vg)。g将dI/dV(V
s, V
g)并排隧道到设备A中相同位置的AA位点和点接触g (V
s, V
g)。
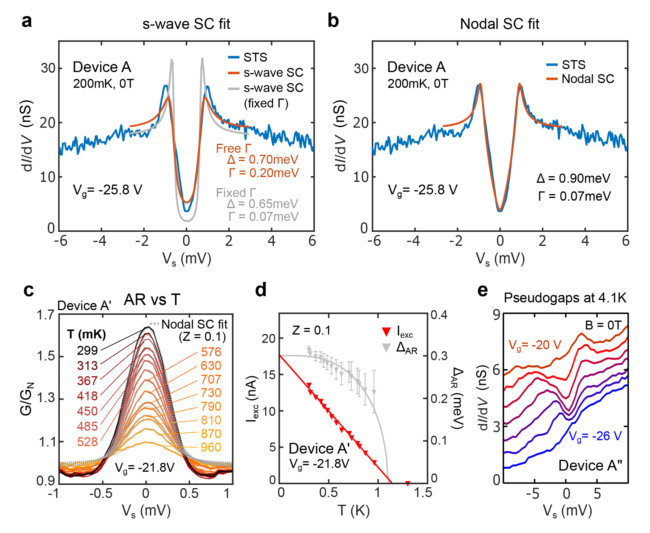
图3 隧道和Andreev反射谱曲线拟合 a dyns -function与Vg = -25.8 V时的实验隧穿光谱吻合b,除了对节点超导体与a相同, c,在300 mK和1 K之间的15个温度下,在Vg = -21.8 V下,A '器件的Andreev反射光谱(实体曲线)与BTK模型(虚线曲线)相吻合d,从BTK中提取的过剩电流Iexc与超导能隙ΔAR吻合曲线。e A器件中在Vg = -20 V和Vg = -26 V之间的AA位点中心获得的隧穿dI/dV(Vs)光谱。
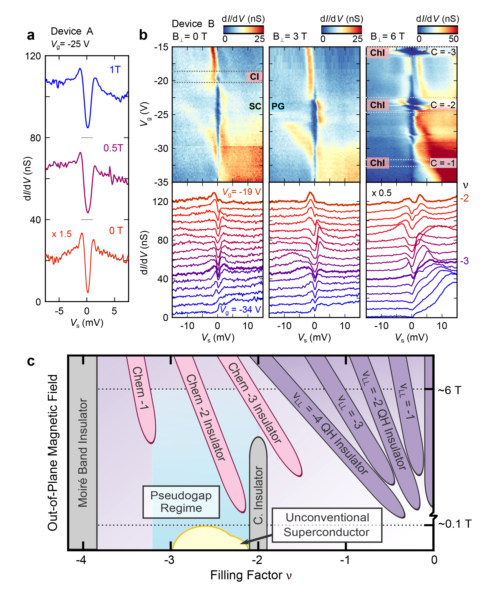
图4. 空穴掺杂MATBG的赝隙状态和相图 a dI / dV,隧道(Vs)光谱Vg = -25 V带的中心一个AA位点在B = 0 T,0.5T,和1 T,显示突出的差距在EF的持久性远高于MATBG. b,对于Vg = -19 V到Vg = -34 V,以及对于b = 0 T, 3 T,和6 T,在b器件AA位点上的隧道dI/dV(Vs, Vg)和dI/dV(Vs)光谱,清晰度曲线偏移7.5 nS。c,在空穴掺杂区域,MATBG作为平带填充因子ν和磁场B的函数的相位示意图。
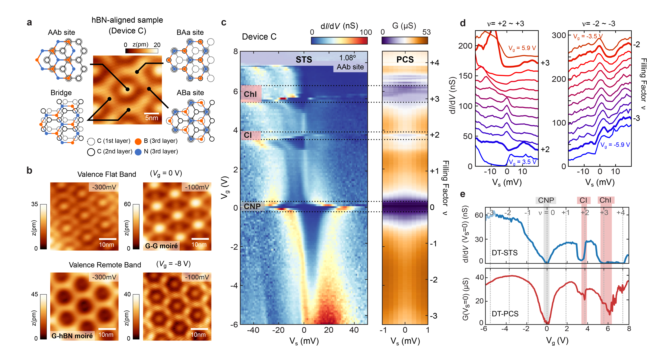
图5 DT-STS和DT-PCS在非超导MATBG上对准hBN a,与底层hBN基底完全相称的MATBG的STM图像。b,不同Vs和Vg值的MATBG与hBN对齐的STM图像, c,将dI/dV(Vs, Vg)引入AAb位点和G(Vs, Vg)的点接触。d,来自c的dI/dV(Vs)光谱,清晰度偏移15 nS(左)和20 nS(右)。e,隧道dI/dV(Vg)和PCS G(Vg)线切割从c为Vs = 0 V。
相关科研成果由美国普林斯顿大学Ali Yazdani等人于2021年发表在Nature(https://doi.org/10.1038/s41586-021-04121-x)上。原文:Evidence for unconventional
superconductivity in twisted bilayer graphene。
转自《石墨烯研究》公众号
.jpg)

 图1 超导MATBG隧穿间隙的扫描隧穿光谱研究 a,实验装置原理图。b, MATBG的STM地形图像。c,在A器件AA位点拍摄的Tunneling dI/dV(Vs, Vg)显示了固定在EF上的传导和价平带。d 器件A的高分辨率dI/dV(Vs, Vg)在ν =-2,和ν =-2与ν =-3之间的间隙。e 在Vg =-22.6 V和Vg =-25.8 V时,器件A的dI/dV(Vs)光谱。f,除B装置(1.06,0.1%应变)外,与d相同。g在Vg =-19.8 V和Vg = -25.6 V时,器件B的dI/dV(Vs)光谱。
图1 超导MATBG隧穿间隙的扫描隧穿光谱研究 a,实验装置原理图。b, MATBG的STM地形图像。c,在A器件AA位点拍摄的Tunneling dI/dV(Vs, Vg)显示了固定在EF上的传导和价平带。d 器件A的高分辨率dI/dV(Vs, Vg)在ν =-2,和ν =-2与ν =-3之间的间隙。e 在Vg =-22.6 V和Vg =-25.8 V时,器件A的dI/dV(Vs)光谱。f,除B装置(1.06,0.1%应变)外,与d相同。g在Vg =-19.8 V和Vg = -25.6 V时,器件B的dI/dV(Vs)光谱。 图2 MATBG的点接触光谱和Andreev反射 a利用密度调谐点接触光谱(DT-PCS)测量安德烈耶夫反射过程的原理图。b设备A在Vs = 0 V时接触点G(Vg)的切线c在0 T和200 mT之间的五种磁场强度下,在Vg = -21 V超导载流子密度范围内点接触G(Vs)谱线切割。d,线切的点接触型G (Vs)光谱, e在50 mT左右Andreev反射消失的面外磁场的不同值的点接触G(Vs, Vg)和dG/ dVs(Vs, Vg)。在1.3 K左右Andreev反射消失的不同温度值的点接触G(Vs, Vg)和dG/dVs(Vs, Vg)。g将dI/dV(Vs, Vg)并排隧道到设备A中相同位置的AA位点和点接触g (Vs, Vg)。
图2 MATBG的点接触光谱和Andreev反射 a利用密度调谐点接触光谱(DT-PCS)测量安德烈耶夫反射过程的原理图。b设备A在Vs = 0 V时接触点G(Vg)的切线c在0 T和200 mT之间的五种磁场强度下,在Vg = -21 V超导载流子密度范围内点接触G(Vs)谱线切割。d,线切的点接触型G (Vs)光谱, e在50 mT左右Andreev反射消失的面外磁场的不同值的点接触G(Vs, Vg)和dG/ dVs(Vs, Vg)。在1.3 K左右Andreev反射消失的不同温度值的点接触G(Vs, Vg)和dG/dVs(Vs, Vg)。g将dI/dV(Vs, Vg)并排隧道到设备A中相同位置的AA位点和点接触g (Vs, Vg)。

 图5 DT-STS和DT-PCS在非超导MATBG上对准hBN a,与底层hBN基底完全相称的MATBG的STM图像。b,不同Vs和Vg值的MATBG与hBN对齐的STM图像, c,将dI/dV(Vs, Vg)引入AAb位点和G(Vs, Vg)的点接触。d,来自c的dI/dV(Vs)光谱,清晰度偏移15 nS(左)和20 nS(右)。e,隧道dI/dV(Vg)和PCS G(Vg)线切割从c为Vs = 0 V。
图5 DT-STS和DT-PCS在非超导MATBG上对准hBN a,与底层hBN基底完全相称的MATBG的STM图像。b,不同Vs和Vg值的MATBG与hBN对齐的STM图像, c,将dI/dV(Vs, Vg)引入AAb位点和G(Vs, Vg)的点接触。d,来自c的dI/dV(Vs)光谱,清晰度偏移15 nS(左)和20 nS(右)。e,隧道dI/dV(Vg)和PCS G(Vg)线切割从c为Vs = 0 V。.jpg)


