通过化学气相沉积法生长的石墨烯中，通常可以观察到各种构型，包括波纹和褶皱。站立的自粘石墨烯褶皱在达到一定高度后会折叠为石墨烯折皱。我们采用连续近似法来预测由不同金属基底支撑的石墨烯折皱的形态。我们的模型基于弹性弯曲和范德华(vdW)相互作用能量的平衡。我们将褶皱的几何形状划分为三个组成部分，并将系统的总能量表示为这三个独立的能量成分的总和。利用变分法将每个能量分量最小化，并推导出对应部分形状的参数解。我们应用6-12 Lennard-Jones势来模拟石墨烯-基底vdW相互作用的强度。当我们考虑折皱的两种潜在构象时，分析显示，折叠的双分子层后面总是跟着一个平坦区域。该模型还预测了自粘褶皱的临界高度，结果与之前的实验和理论数据一致。该模型还预测了自粘褶皱的临界高度，提供了与先前关于该过渡高度的实验和理论数据一致的结果。
 
  
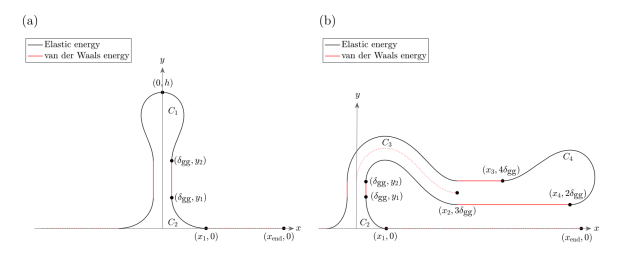
图1. (a)自粘的石墨烯褶皱和(b)折叠的石墨烯褶皱，支撑在基板上的几何图形示意图。
 
  
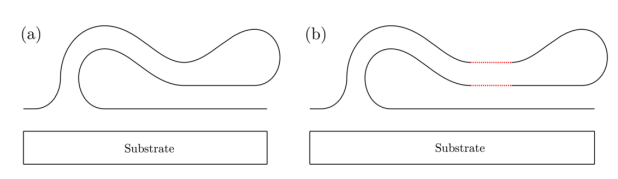
图2. 折皱的两种潜在构象的结构图示:(a)构象A和(b)构象B，与折叠的双分子层的距离分别为零和非零。
 

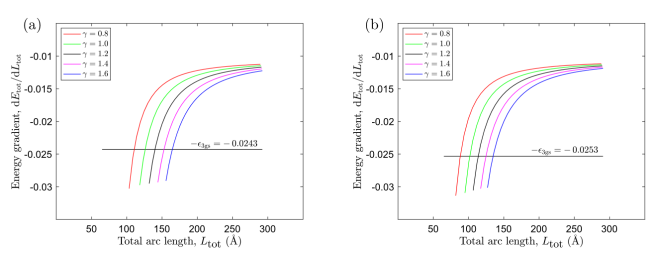
图3.能量梯度是由(a)Cu(111)基底和(b) Ni(111)基底支撑的折皱的总弧长L_tot的函数。彩色线表示构象A的能量梯度，黑线表示构象B的能量梯度，其中交点给出了构象A每个γ值的长度L_B。              
 

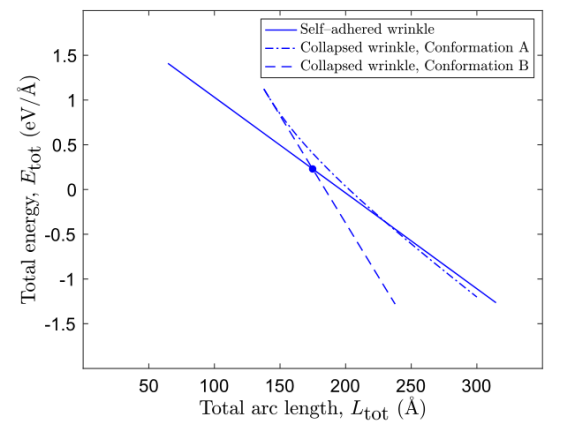
图4.对于Cu（111）基底支撑的弯曲刚度为γ=1.2 eV的不同褶皱结构，总能量E_tot的行为与总弧长L_tot有关。标记点表示临界长度L_crit，其中自粘褶皱折叠并遵循构象B。
 
  
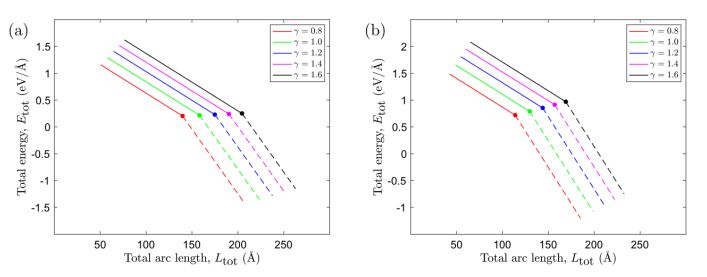
图5. 总能量E_tot的行为与自粘褶皱（实线）和折皱构象B（虚线）的总弧长L_tot有关，其中：(a)Cu(111)基底和(b) Ni(111)基底支撑。标记点表示临界长度L_crit，其中自粘褶皱折叠并遵循构象B。
 
 
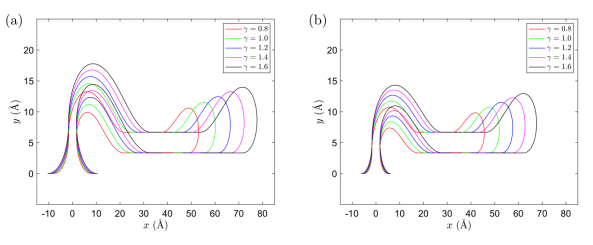
图6. 在L_tot=L_crit的情况下，不同弯曲刚度的(a)Cu(111)基底和(b) Ni(111)基底上支撑的折皱构象。
 

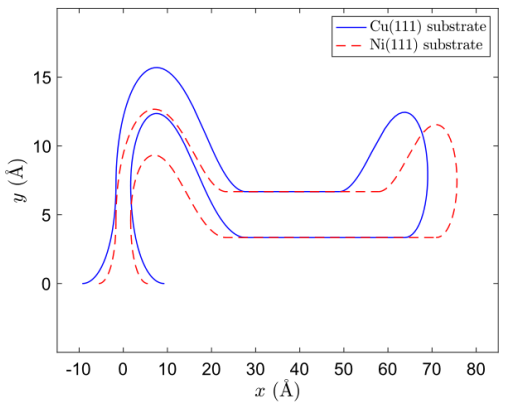
图7. 固定弧长L_tot=180Å和弯曲刚度γ=1.2 eV的Cu(111)和Ni(111)基底上支撑的折皱构象。

       相关研究成果由阿卜杜勒阿齐兹国王大学应用学院、阿德莱德大学数学科学学院的Jabr Aljedani等人于2021年发表在Applied Physics A (https://doi.org/10.1007/s00339-021-05000-y)上。原文：Variational model for collapsed graphene wrinkles。

转自《石墨烯研究》公众号