本研究采用一阶剪切变形理论（FSDT）建立了功能梯度石墨烯板增强复合材料(FG-GPLRC)截锥壳的非线性动力学模型。对FG-GPLRC截锥壳进行了振动分析。考虑到FG-GPLRC截锥壳的石墨烯片(GPLs)具有三种不同的分布模式，采用改进的Halpin-Tsai模型计算有效杨氏模量。利用Hamilton原理、FSDT和von Karman型非线性几何关系推导了FG-GPLRC截锥壳的偏微分控制方程组。采用伽辽金法求解截锥壳的常微分方程。然后，采用谐波平衡法求解FG-GPLRC截锥壳的解析非线性频率。讨论了FG-GPLRC截锥壳的质量分数、GPLs分布形式、长径比、径厚比等因素对其非线性固有频率特性的影响。这项研究最终发现了FG-GPLRC截锥壳的周期运动和混沌运动。
 
 
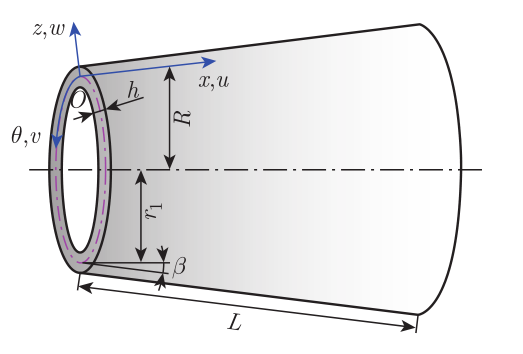
图1. FG-GPLRC截锥壳模型及曲线坐标系。
 
 
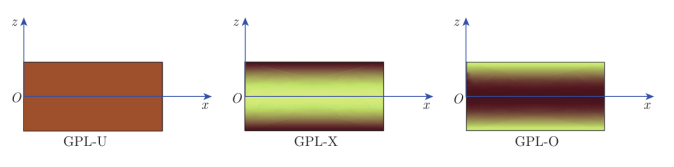
图2. FG-GPLRC材料中三种GPLs的分布模式。
 

图3. FG-GPLRC截锥壳GPLs的体积分数。
 

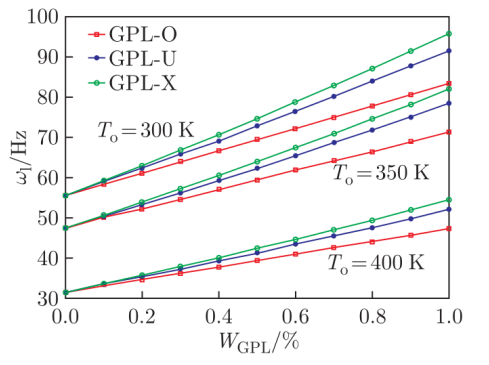
图4. FG-GPLRC截锥壳的线性基本固有频率。
 

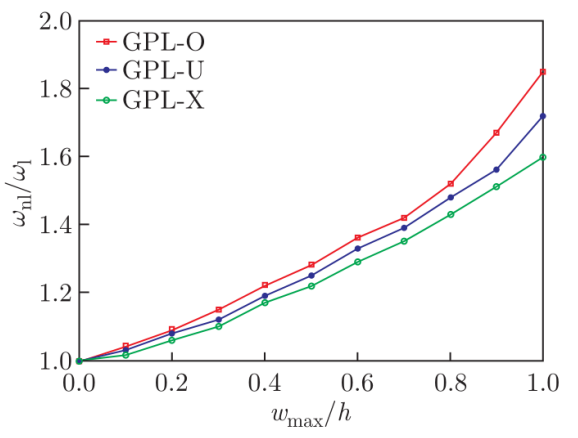
图5. FG-GPLRC截锥壳最大振幅对非线性基频与线性基频之比的影响。
 

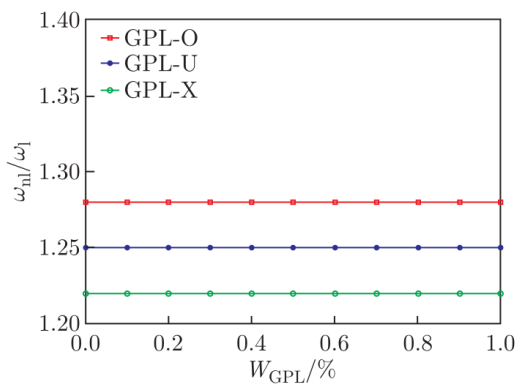
图6. FG-GPLRC截锥壳中GPLs重量分数对非线性基频与线性基频之比的影响。
 

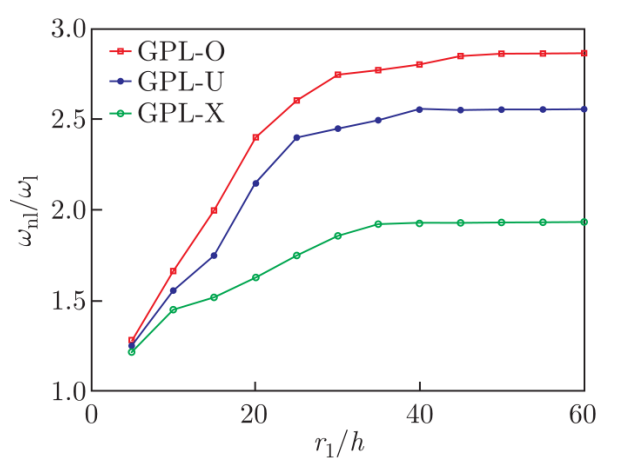
图7. FG-GPLRC截锥壳的径厚比r₁/h对非线性基频与线性基频之比的影响。
 

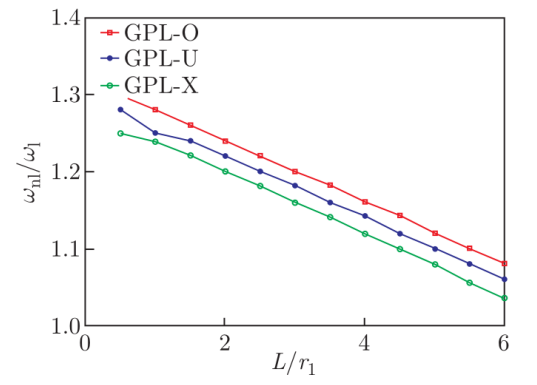
图8. FG-GPLRC截锥壳长径比L/r₁对非线性基频与线性基频之比的影响。
 

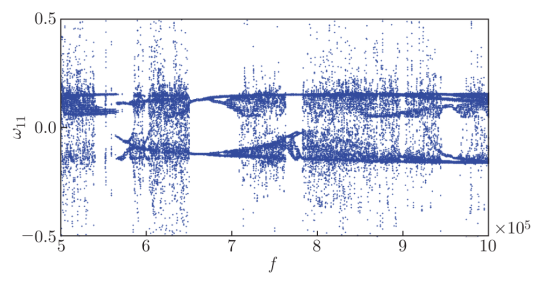
图9. FG-GPLRC截锥壳横向激励与第一模态振幅的分岔图。
 
 
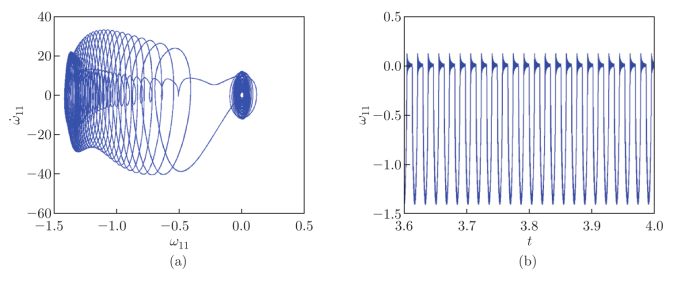
图10. FG-GPLRC截锥壳在f=6.3x10⁵时的周期运动：(a)相位图和(b)时程图。 
 

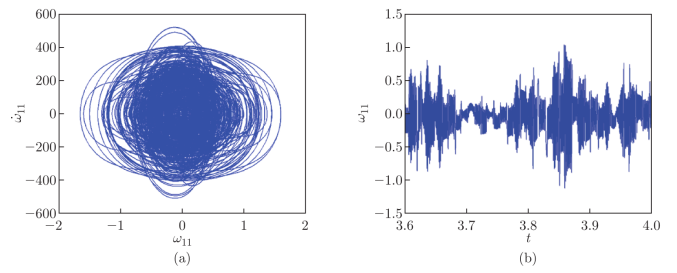
图11. FG-GPLRC截锥壳在f=6.6x10⁵时的混沌运动：(a)相位图和(b)时程图。 
 
       相关研究成果由北京信息科技大学机械工程学院Shaowu YANG等人于2021年发表在Applied Mathematics and Mechanics (https://doi.org/10.1007/s10483-021-2747-9)上。原文：Nonlinear vibration of functionally graded graphene platelet-reinforced composite truncated conical shell using first-order shear deformation theory。

转自《石墨烯研究》公众号