超薄石墨烯基膜已显示出高性能纳米机电（NEMS）器件的巨大前景。此类膜建模的关键挑战在于，它们通常在不满足“纯弯曲”或“纯拉伸”假设或近似值的偏转状态下运行。本研究基于Föppl–von Kármán（FvK）方程提出了石墨烯-聚合物异质结构（GPH）NEMS膜模型，该模型同时考虑了弯曲力和拉伸力。通过原子力显微镜形貌图获得的实验GPH膜形状与基于FvK的有限元方法模拟预测的膨胀形状进行了比较，它们彼此之间显示出极好的一致性。当在电容式压力传感器配置中GPH膜在压力下偏转时，通过准确预测偏转GPH膜装置在变化压力下的电容变化，进一步证明了该模型的有效性。该模型在基于石墨烯的NEMS器件的设计和开发中是一个强大的新工具，能够预测石墨烯NEMS器件性能或帮助设计器件几何结构以匹配所需性能。
 
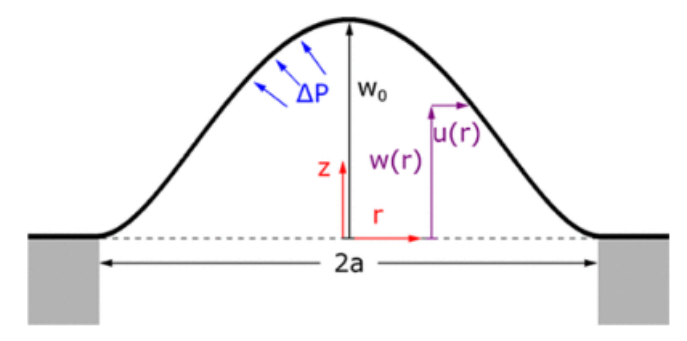
图1.充气轴对称膜的横截面示意图和膜上的压差。
 
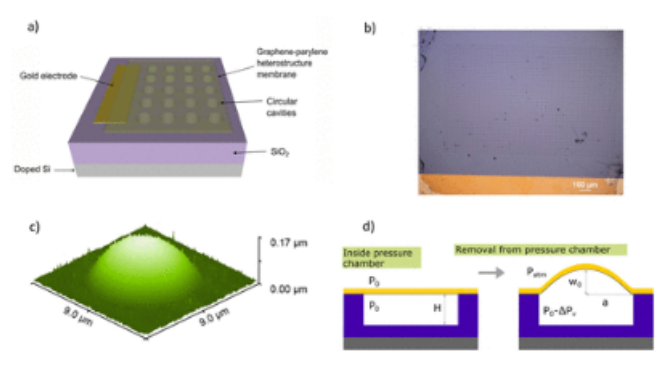
图2. 传感器设计和微泡膨胀测试。（a） GPH膜电容式压力传感器的3D示意图。（b） 用于测量电容压力响应的GPH膜电容压力传感器的光学显微照片，包括金电极、GPH膜和空腔。（c） 膨胀泡罩的3D地形原子力显微镜（AFM）图像，半径a=3.5μm，厚度t=45 nm，压力ΔP=0.94 kPa。（d）2D示意横截面图，描绘了具有单个空腔和致动膜的微泡膨胀测试程序，标记了重要参数。
 
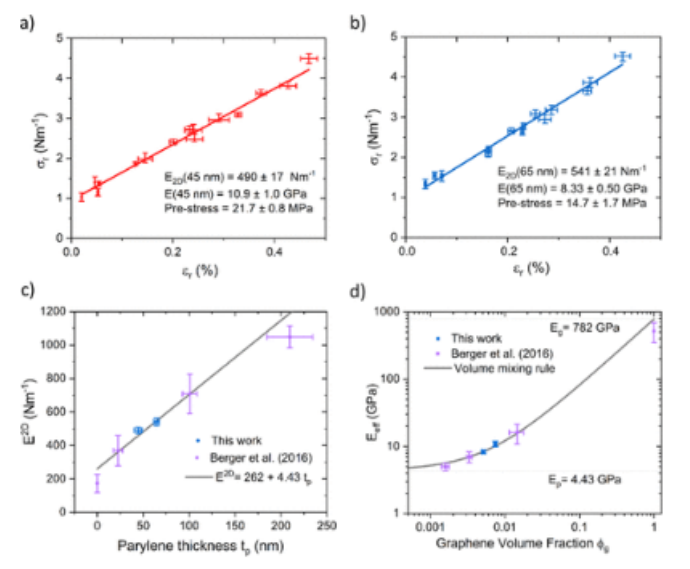
图3. 微泡膨胀测试结果。（a，b）厚度为（a）45和（b）65 nm的GPH膜的径向应力-应变图，以及通过拟合从图中提取的量（E、E^2D和预应力）。（c）测量E^2D与聚对二甲苯厚度，。对于本工作中的数据，y误差条来自（a，b）的线性回归中的不确定性。x误差条是七个厚度测量值的标准偏差。（d）GPH膜的有效体积模量是石墨烯体积分数的函数，符合体积混合规则。两条水平虚线表示提取的石墨烯和聚对二甲苯的体积模量。通过组合（a，b）的线性回归中的误差和膜厚度的不确定度来量化误差条。Berger等人（2016）的数据误差条通过结合所述E2D和膜厚度不确定度中的所述不确定度进行量化。
 
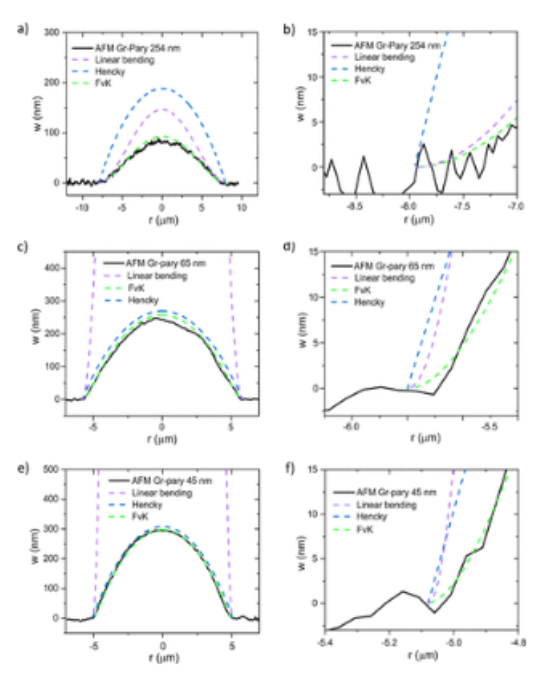
图4. 与线性弯曲、Hencky解和FvK模型相比，GPH膜相对于径向位置的偏转。（a） 254 nm的膜厚加压至ΔP=21 kPa。（b） 夹紧膜边缘周围（a）的放大。（c） 65 nm的厚度加压至ΔP=68 kPa。（d） 夹紧膜边缘周围（b）的放大。（e） 加压至ΔP=116 kPa的45 nm厚度。（f） 夹紧膜边缘周围（e）的放大。
 
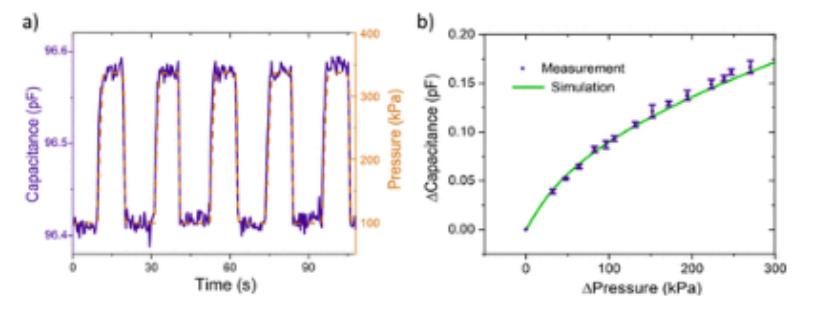
图5. 电容–GPH电容式压力传感器的压力响应。（a） 在340 kPa至大气压的五个压力循环中，设备电容和外部压力随时间绘制。（b） 作为压力变化函数的平均电容变化图，将FvK FEM模拟与测量进行比较。误差条是九个读数的标准偏差。
 
       相关研究成果由曼彻斯特大学Aravind Vijayaraghavan 等人2023年发表在ACS Applied Materials & Interfaces (https://doi.org/10.1021/acsami.2c21096)上。原文：Modeling Graphene–Polymer Heterostructure MEMS Membranes with the Föppl–von Kármán Equations。

转自《石墨烯研究》公众号