基于石墨烯的高质量二维电子系统已成为研究超导性的高度可调平台。具体来说，在电子和空穴掺杂的扭曲石墨烯摩尔体系中都观察到了超导现象，而在晶体石墨烯体系中，迄今为止只在空穴掺杂的斜方三层石墨烯（RTG）和空穴掺杂的Bernal双层石墨烯（BBG）中观察到了超导现象。最近，由于靠近单层 WSe₂，BBG 的超导性得到了增强。在此，报告了通过静电掺杂在电子和空穴掺杂的 BBG/WSe₂ 器件中观察到的超导性和一系列味道对称性破坏相。观察到的超导电性的强度可通过施加垂直电场进行调节。电子掺杂和空穴掺杂超导的最大别列津斯基-科斯特利兹-无穷大转变温度分别约为 210 mK 和 400 mK。只有当外加电场将 BBG 电子或空穴波函数驱向 WSe₂ 层时，超导性才会出现，这突出了 WSe₂ 层在观测到的超导性中的重要性。掺杂空穴的超导违反了保利顺磁极限，与类伊辛超导体一致。相比之下，电子掺杂的超导电性遵守了保利极限，尽管在导带中也有显著的近似伊辛自旋轨道耦合。本研究的发现凸显了 BBG 中与传导带相关的丰富物理现象，为进一步研究晶体石墨烯的超导机制和开发基于 BBG 的超导体设备铺平了道路。
 

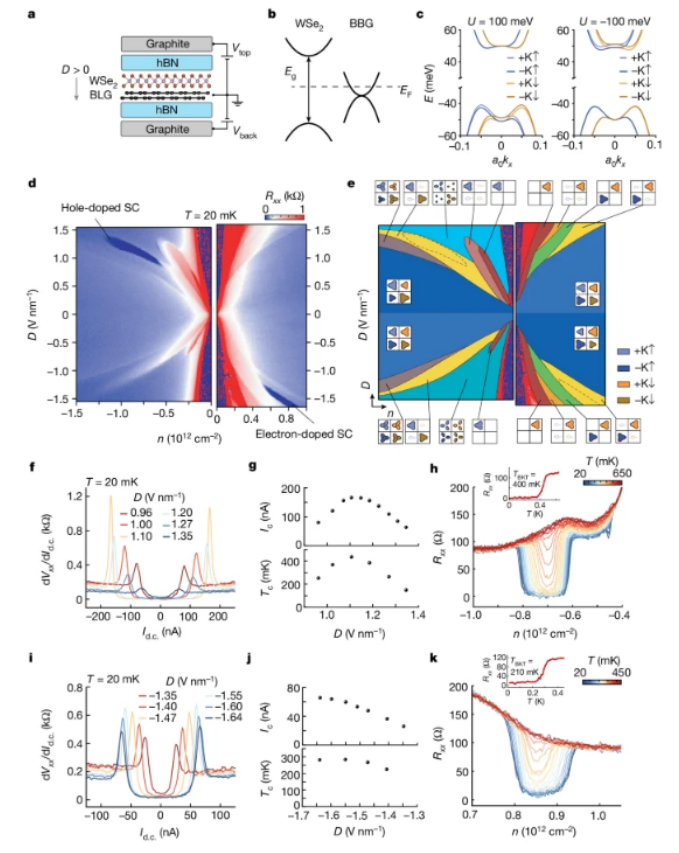
图1. BBG/WSe₂的相图及电子和空穴掺杂的超导性。a. BBG/WSe₂ 双栅器件示意图。 b. D = 0 V nm^-1 时单层 WSe₂ 和 BBG 的带排列示意图。BBG 的电荷中性点位于 WSe₂ 半导体带隙深处。c. 层间电位差 U = ±100 meV（大致相当于位移场 D≈ ±1 V nm^-1）时布里渊区 K 点和 K′点附近的单粒子带结构计算结果。在正 D 时，空穴波函数集中在 BBG 的顶层，因此 WSe₂- 引发的 SOC 在价带中更为突出。在负 D 时，电子波函数集中在 BBG 的顶层，因此 WSe₂-诱导的 SOC 在导带中更为突出。 d. 在 T = 20 mK 时测量的 Rxx-D-n 图，涵盖了电子掺杂（0 < n < 1.0 × 10¹² cm^-2, -1.65 V nm^-1 < D < 1.60 V nm^-1）和空穴掺杂（-1.5 × 10¹² cm^-2 < n < 0, -1.55 V nm^-1 < D < 1.55 V nm^-1）区域。e. 根据 d 和量子振荡的 FFT 分析确定的实验相图。我们使用 d 中的 R_xx 特征作为相界。假定自旋轨道耦合不混合，通过对量子振荡的 FFT 分析，推断出每个相位可能的费米面结构（如示意图所示）。(f)i，不同 D 时空穴（f）和电子掺杂超导（i）的 dV_xx/dI_d.c. 与 I_d.c. 的关系。g,h,j,k，空穴超导（g）和电子掺杂超导（j）的 I_c（上）和 T_c（下）与 D 的关系，以及掺空穴一侧在 D = 1.1 V nm^-1 时（h）和掺电子一侧在 D = -1.64 V nm^-1 时（k）的 R_xx 与 n 的温度关系。插图显示了最佳掺杂状态下 R_xx 与 T 的关系曲线，此时 T_c 达到最高值。
 
 
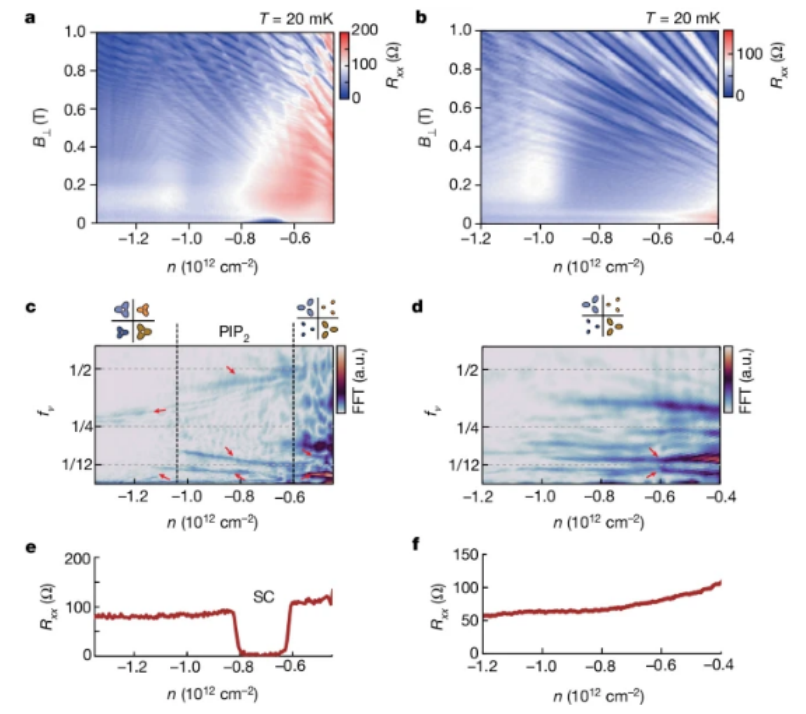
图2. 掺孔超导的费米面分析。a,b，D = 1.1 V nm^-1 (a) 和 1.5 V nm^-1 (b) 时掺杂空穴一侧的 Rxx 与 n 和 B_⊥ 的关系。c,d，D = 1.1 V nm^-1 (c) 和 1.5 V nm^-1 (d) 时掺杂空穴一侧的 R_xx (1/B_⊥) 与 n 和 f_ν 的 FFT 关系。c 和 d 中的 FFT 分析分别基于 0.2 T < B_⊥ < 1 T 范围内的 R_xx 数据。不同相位的费米面结构示意图也显示在 c 和 d 中。不同相位的 FFT 频率峰值用红色箭头标出。在 D = 1.1 V nm^-1 时，在 PIP₂ 相内靠近三方翘曲相的位置观察到一个超导区 (SC)，该超导区由 Ising SOC 诱导的自旋分裂形成。
 

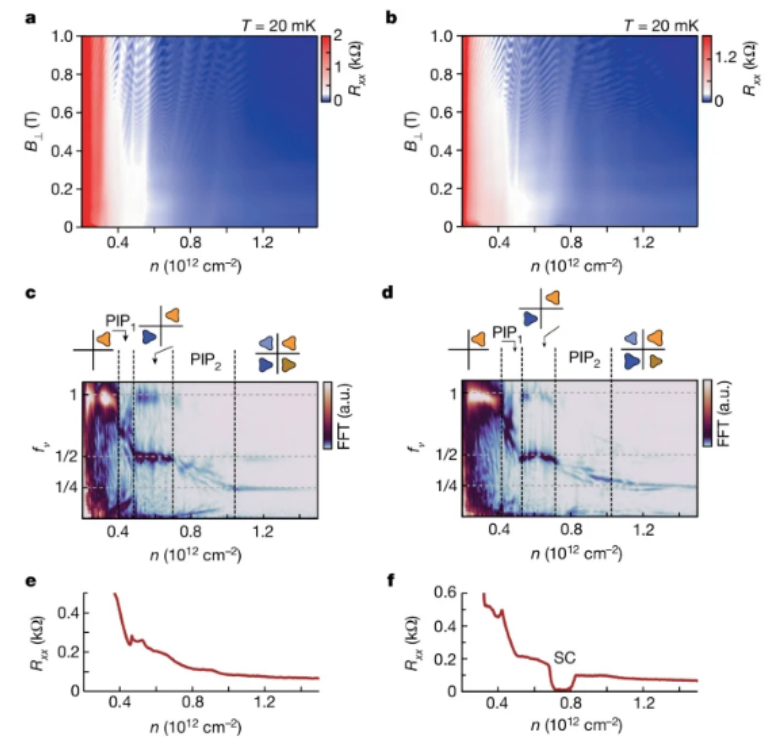
图3. 电子掺杂超导电性的费米表面分析。a,b，D = 1.55 V nm^-1 (a) 和 -1.55 V nm^-1 (b) 时电子掺杂侧的 R_xx 与 n 和 B_⊥ 的关系。c,d，D = 1.55 V nm^-1 (c) 和 -1.55 V nm^-1 (d) 时电子掺杂侧的 R_xx (1/B_⊥) 与 n 和 f_ν 的 FFT 关系。c 和 d 中的 FFT 分析分别基于 a 和 b 中 0.2 T < B_⊥ < 1 T 范围内的 R_xx 数据。c 和 d 中还显示了不同相的费米面结构示意图。e, f，掺电子一侧在 B = 0 T、D = 1.55 V nm^-1 时（e）和-1.55 V nm^-1 时（f）的 R_xx 与 n 的关系。只有在负 D 时才能观察到电子掺杂超导现象。
 

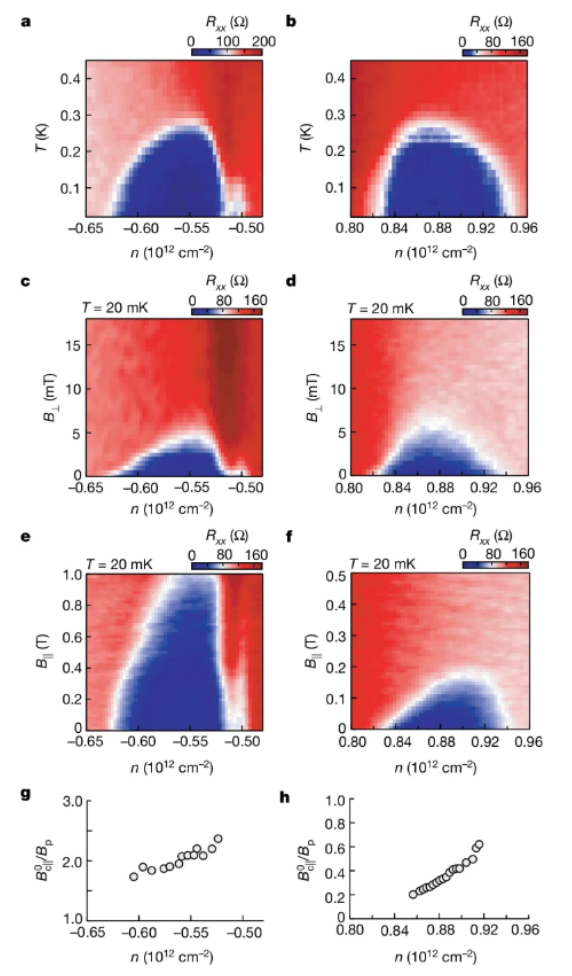
图4. 空穴掺杂和电子掺杂超导电性的面内磁场依赖性。a,b，掺空穴超导圆顶（a）和掺电子超导圆顶（b）分别在 D = 0.96 V nm^-1 和 D = -1.64 V nm^-1 时 R_xx 与 T 和 n 的函数关系。c,d，掺空穴超导圆顶（c）和掺电子超导圆顶（d）分别在 D = 0.96 V nm^-1 和 D = -1.64 V nm^-1 时 R_xx 与 B_⊥ 和 n 的函数关系。e,f, R_xx 分别是 D = 0.96 V nm^-1 (e) 和 D = -1.64 V nm^-1 (f) 时 B∥ 和 n 的函数。在最佳掺杂条件下，空穴掺杂超导在 B∥ 高达 1 T 的条件下仍然可以存活，而在 D = -1.64 V nm^-1 条件下，整个电子掺杂超导圆顶在 B∥ ≈ 0.2 T 的小条件下被完全抑制。g,h， Pauli不相容率B⁰_c||/B_p 分别为 D = 0.96 V nm^-1 (g) 和 D = -1.64 V nm^-1 (h)时的Pauli不相容率与 n 的关系。误差带在圆圈范围内。掺空穴的超导违反了保利极限，而掺电子的超导则遵守了保利极限。此外B⁰_c||/B_p 在掺空穴和掺电子超导中都表现出与密度相关的行为。
 
      相关研究成果由武汉大学Fengcheng Wu和上海交通大学Xiaoxue Liu、Tingxin Li等人2024年发表在Nature (链接：https://www.nature.com/articles/s41586-024-07584-w)上。原文：Tunable superconductivity in electron- and hole-doped Bernal bilayer graphene

转自《石墨烯研究》公众号