锯齿形石墨烯纳米带（ZGNRs）中π电子的拓扑设计产生了丰富的磁量子现象和奇异量子相。对称ZGNR通常显示反铁磁耦合自旋有序边态。消除ZGNRs中的交叉边磁耦合不仅可以实现一类铁磁量子自旋链，在一维极限中探索量子自旋物理和多个量子位的纠缠，而且还建立了一个广受追捧的碳基铁磁输运通道，对GNR基量子电子学的最终定标至关重要。在这里，本研究报告了一种设计和制造具有两种不同边缘结构的Janus GNR（JGNR）形式的铁磁GNR的一般方法。在Lieb定理和拓扑分类理论的指导下，我们设计了两个JGNR，在保持相对的锯齿边不变的情况下，在一条锯齿边上不对称引入苯基序的拓扑缺陷阵列。这打破了结构对称性，并在每个单位细胞内产生子晶格不平衡，从而引发自旋对称性的破坏。设计了三个Z形前驱体，分别制备了一个ZGNR母体和两个JGNR母体，缺陷阵列具有最佳的晶格间距，使得缺陷边缘的磁边缘态完全猝灭。通过扫描探针显微镜、光谱学和第一性原理密度泛函理论对JGNRs进行表征，证实了JGNRs的成功制备，其铁磁基态沿着原始的锯齿形边缘分布。
 
 
 
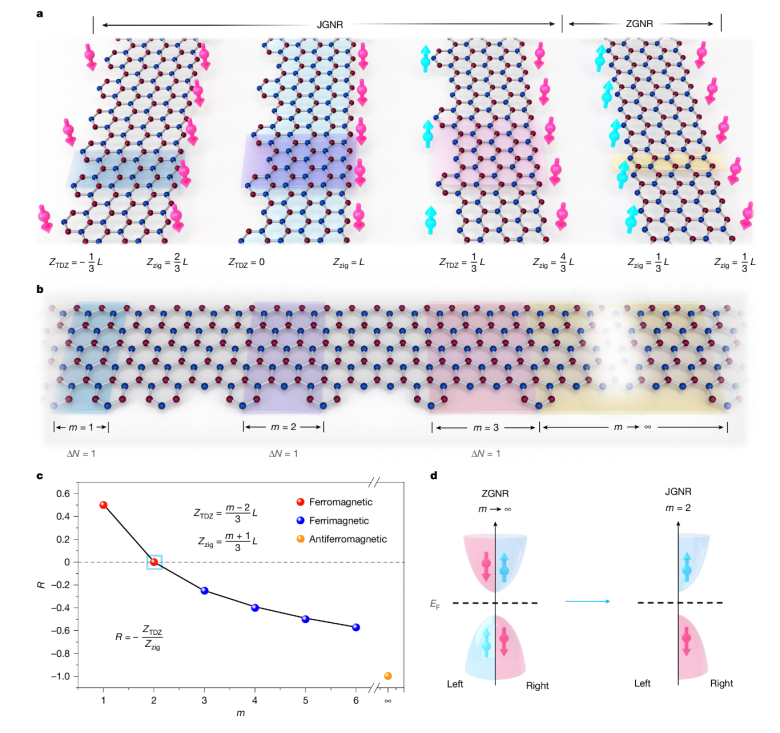
图1. a 具有不同m值的不同TDZ边的JGNR示意图。红色和蓝色箭头分别表示边缘状态的自旋向上和自旋向下（按惯例）。底部的数字表示相应TDZ（Z_TDZ）和完整锯齿（Z_zig）边的CPI指数，其中L是沿锯齿方向的有限长色带的单位单元数（单位单元用颜色着色）。红色和蓝色原子是来自两个不同亚晶格的碳原子。b、 JGNRs重复单元示意图，说明相邻苯环之间的“缺陷”位置间距逐渐增大，从左到右依次为：1、2、3和无穷大（∞）。除了m = ∞.c，两条边之间的m依赖磁序，每个单元的子晶格不平衡度在所有情况下都保持为ΔN = 1，这可以使用JGNRs两条边的CPI指数比率的负号来描述（定义为R =  -（Z_TDZ/Z_zig））。当m增大时，R从正值变为负值，在m =2处穿过0。根据Lieb定理和CPI理论，JGNR通过铁磁耦合区域经历从铁磁到反铁磁的转变。d、 ZGNR（m = ∞）基带隙附近自旋极化能带结构示意图 , 两条对称锯齿形边之间的反铁磁耦合（铁磁有序）到JGNR（m = 2, 仅在单个锯齿形边缘处的铁磁有序）。
 
 
 
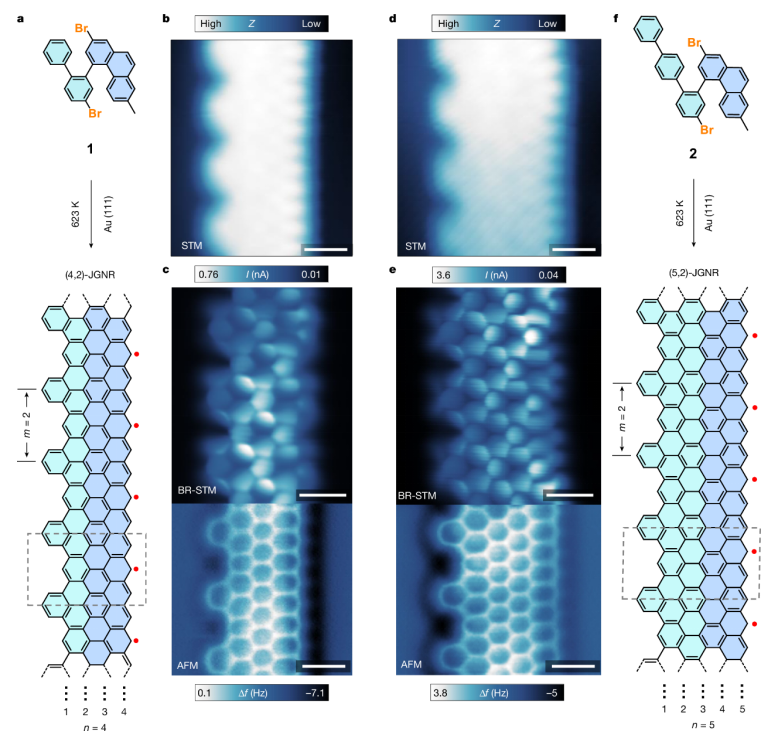
图2: a、 （4,2）-JGNR的表面合成策略。b、 （4,2）-JGNR的恒定电流STM图像（V_s = −800 mV，I_t = 200 pA；其中V_s是样品偏置，它是隧道电流）。c、 （4,2）的BR-STM图像（V_s = −10 mV）和nc-AFM图像（V_s= 10 mV）-JGNR在恒定高度模式下使用具有共同功能化尖端的qPlus传感器获取。d、 （5,2）-JGNR的恒定电流STM图像（V_s = −800 mV，I_t = 200 pA）。e、 （5,2）-JGNR的BR-STM图像（V_s = −10 mV）和nc-AFM图像（V_s = 10 mV）在恒定高度模式下使用具有共同功能化尖端的qPlus传感器获取。f、 （5,2）-JGNR的表面合成策略。比例尺，5 Å（b–e）。
 


图3. a、 5-ZGNRs的表面合成策略。b、 5-ZGNR的恒流STM图像（V_s = −800 mV，I_t = 200 pA）c，5-ZGNR在Au（111）上的dI/dV点光谱，在插图（红十字）中标记的位置。虚线显示Au（111）参考光谱（调制电压V_ac = 20 mV）。插图：使用qPlus传感器在恒定高度模式下获取的nc-AFM图像，该传感器具有协同功能化的尖端（V_s = 10 mV）。d–f，在+750 mV（d）的电压偏置下记录的恒定电流dI/dV图，-225mv（e）和−470mv（f）。V_ac = 10 mV。注意到边缘态的dI/dV图中的轻微不对称可能是由尖端不对称引起的。g–i，DFT计算DOS光谱A′（g）、B′（h）和C′（i）能量位置处的LDO，如k所示。LDO在5-ZGNR原子平面以上4 Å高度处计算。j、 5-ZGNR的BR-STM图像（V_s= 10 mV）。k、 DFT计算的自旋上升（红色）和自旋下降（蓝色）的DOS对一个独立的5-ZGNR（加宽27 meV高斯）显示了一个330 meV的模拟能隙（ΔE_sim）。l、 用密度泛函理论计算了一个独立的5-ZGNR的能带结构。插图：计算的自旋密度分布。比例尺，5 Å（b–d，j）。
 


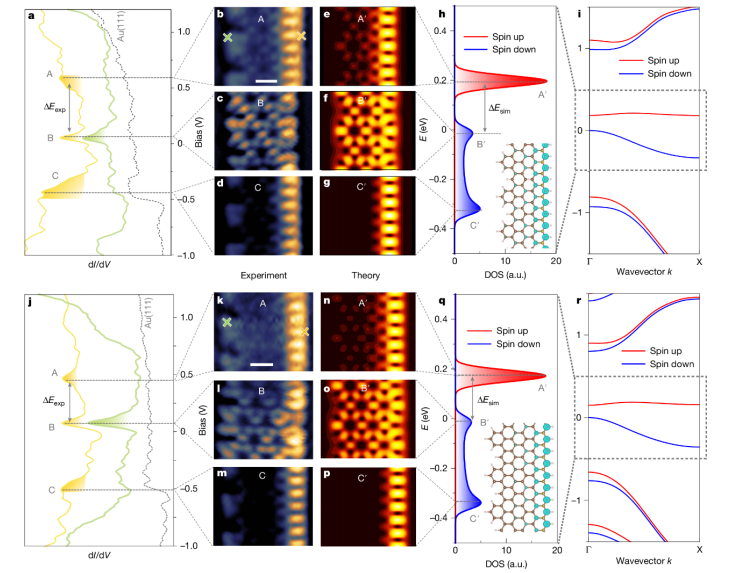
图4. a、（4,2）-JGNR在Au（111）上的dI/dV点光谱，在b（黄色和绿色交叉）标记的相应有色位置。虚线显示Au（111）参考光谱（V_ac = 20 mV）。b–d，在图a（V_ac = 10 mV）中A（b）、b（c）和c（d）能量位置记录的恒流dI/dV图。e–g，DFT计算了在h中标记的A′（e）、B′（f）和C′（g）的能量位置处的LDO。LDO是在（4,2）-JGNR原子平面上方4 Å的高度处计算的。h、 DFT计算了一个独立的（4,2）-JGNR（展宽27 meV高斯）的自旋上升（红色）和自旋下降（蓝色）的DOS。插图：计算的自旋密度分布。i、用DFT方法计算了（4,2）-JGNR的能带结构。j、（5,2）-JGNR在Au（111）上k（黄色和绿色交叉）标记的相应有色位置的dI/dV点光谱。虚线显示Au（111）参考光谱（V_ac= 20 mV）。k–m，在A（k）、B（l）和C（m）能量位置记录的恒定电流dI/dV图，单位为j（V_ac = 10 mV）。n–p。在q中标记的A′（n）、B′（o）和C′（p）的能量位置计算的DFT LDOS。LDOS是在独立（5,2）-JGNR的原子平面上方4 Å的高度计算的。q、计算了（5,2）-JGNR自旋上升（红色）和自旋下降（蓝色）的DFT DOS。插图：计算的自旋密度分布。r、 用密度泛函理论计算了（5,2）-JGNR的能带结构。比例尺，5 Å（b，k）。
 
        相关研究成果由京都大学 Hiroshi Sakaguchi、加利福尼亚大学Steven G. Louie和新加坡国立大学Jiong Lu等人2025年发表在Nature (链接: https://www.nature.com/articles/s41586-024-08296-x)上。原文：Janus graphene nanoribbons with localized states on a single zigzag edge

转自《石墨烯研究》公众号