超导体的宏观量子特性稳健性可通过超流刚度ρ_s这一物理量进行表征，该参数描述了改变宏观量子波函数相位所需能量。在铜基高温超导体等非常规超导体系中，由于动量空间无隙点（节点）引发的准粒子激发，其ρ_s的低温行为显著区别于常规超导体。针对新近发现的魔角扭曲石墨烯体系研究不仅揭示了超导态的存在，更观察到与自发对称性破缺相关的强关联电子态，这为通过ρ_s研究探索其超导态的潜在非常规特性提供了契机。本研究报道了魔角扭曲三层石墨烯（TTG）中超流刚度ρ_s的精确测量，揭示了具有节点能隙特征的非常规超导态。通过射频反射测量技术对耦合微波谐振器的超导TTG样品进行动力学电感响应检测，研究发现了两个关键实验证据：(1) ρ_s在低温区呈现线性温度依赖特性；(2) 电流偏置依赖关系中存在非线性迈斯纳效应。这些现象共同指向超导序参量中存在节点结构特征。进一步的空穴掺杂依赖性分析表明，零温极限下的ρ_s与超导转变温度Tc呈线性关联，此规律与铜基超导体中的Uemura标度关系高度相似，提示体系可能存在相位相干性主导的超导机制。本工作通过多维度实验证据确证了TTG体系中节点超导态的存在，为理解此类石墨烯基超导材料的微观机制确立了关键约束条件。研究采用的微波量子传感技术为二维量子材料的宏观量子特性表征提供了新的方法论框架。
 
 
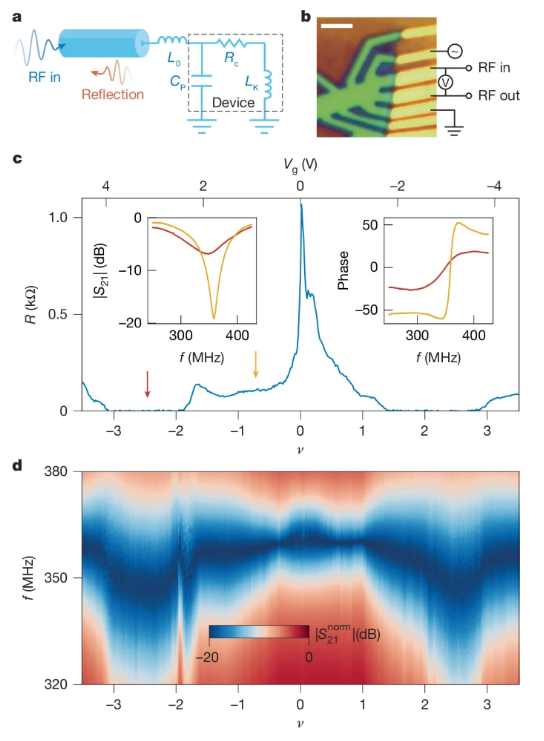
Fig 1.实验装置与器件表征a. 射频反射测量装置原理图。由L₀（匹配电感）与C_P（寄生电容）构成的电感-电容（LC）匹配网络，将器件阻抗（1-10千欧）转换为射频测量电路的50欧特征阻抗。b. 正文所述TTG器件的光学显微图像及简化测量方案示意图。比例尺：3 μm。c. 器件直流电阻R随莫尔填充因子ν的变化关系。样品在电子掺杂区（ν>0）与空穴掺杂区（ν<0）均呈现超导态（R=0）。插图为复反射系数S₂₁的幅值与相位响应，显示正常态与超导态间的谐振频率偏移。d. 归一化振幅随频率 |S₂₁^norm| f与填充因子ν变化的二维映射图。为增强可视化效果，每个ν对应的振幅均经过基线扣除处理。|S₂₁^norm(f)|=1−(max(|S₂₁(f)|)−|S₂₁(f)|)/0.9,当样品从正常态转变为超导态时，谐振器发生约10-15兆赫兹的显著频率偏移（Δf_r）。
 
 
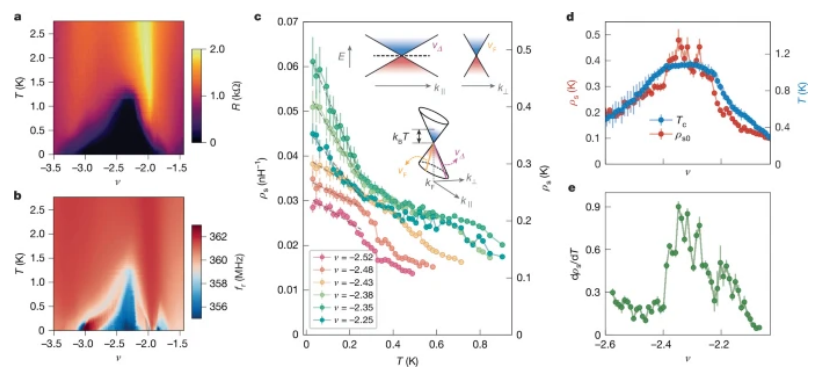
Fig 2.温度与掺杂依赖的超流刚度特性a-b. 莫尔填充因子ν与温度T二维相图：(a) 直流电阻R的演化规律，(b) 谐振器频率f_r的响应映射。超导相变边界呈现显著的温度依赖特性。c. 以ν=-2.4为中心的填充因子区域内，超流刚度ρ_s随温度T的变化曲线。插图：能隙节点附近准粒子的低能色散关系示意图。上方两幅子图分别展示沿费米面平行方向k_∥与垂直方向k_⊥的色散关系，其斜率由Δ能隙速度v_Δ与费米速度v_F共同决定，形成各向异性锥形色散结构（下方示意图）。虚线标示费米能级，蓝色与红色分别表示能量在±k_BT范围内的激发准粒子与准空穴，k_F对应节点所处的费米动量。d. 左轴：通过(c)中曲线线性外推获得的零温超流刚度ρ_s(0)随ν的变化趋势。右轴：基于直流电阻测量确定的超导转变温度T_c随ν的演化规律。e. 低温区超流刚度温度导数dρ/dT随掺杂浓度的变化关系，揭示节点超导态的特征能量尺度。
 
 
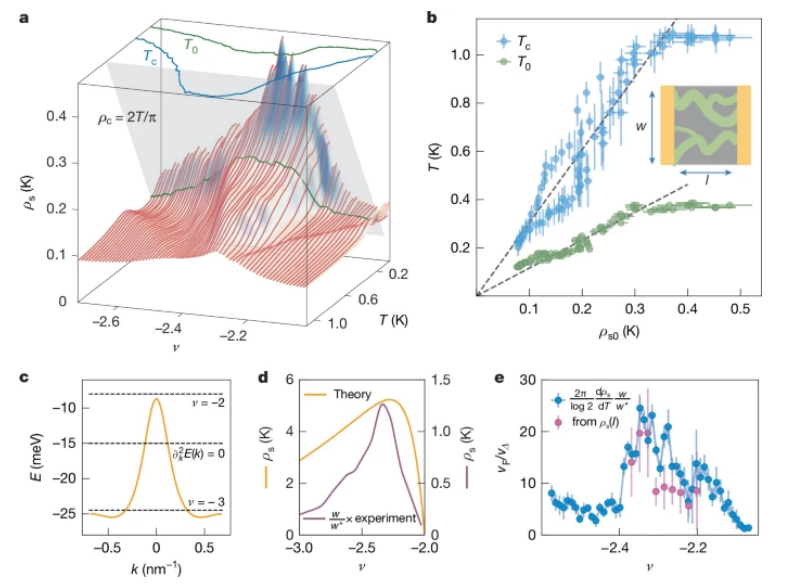
Fig 3. BKT相变、Uemura标度关系与节点配对对称性a. 超流刚度ρ_s随温度T与填充因子ν演化的瀑布图。为提升可视化效果，沿温度轴采用六点移动平均法进行插值平滑处理。通过实验刚度曲线与普适BKT平面（ρ_c=2T/π）的交点确定Berezinskii-Kosterlitz-Thouless（BKT）相变温度T₀。b. T_c与T₀随零温超流刚度ρ_s0的变化关系。插图：可能导致超流刚度低估的非均匀超导路径示意图。c. 魔角扭曲三层石墨烯（TTG）中Hartree-Fock重整化能带在mini-Brillouin区内的动量k依赖关系。虚线标注ν = -2、ν = -3对应的能级及∂_k²E(k)=0曲率反转点。d. 基于Hartree-Fock重整化能带的理论预测ρ_s0(ν)与实验测量值的对比（后者经插值平滑处理）。理论与实验均呈现钟型依赖关系，最大偏移值出现在ν=-2处，但理论值系统性高估约5倍。e. 通过温度依赖ρ_s(T)与电流偏置依赖ρ_s(I)两种方法获得的v_F/v_Δ比值随ν的变化趋势，二者在v_F/v_Δ≈2-20范围内基本吻合。
 
 
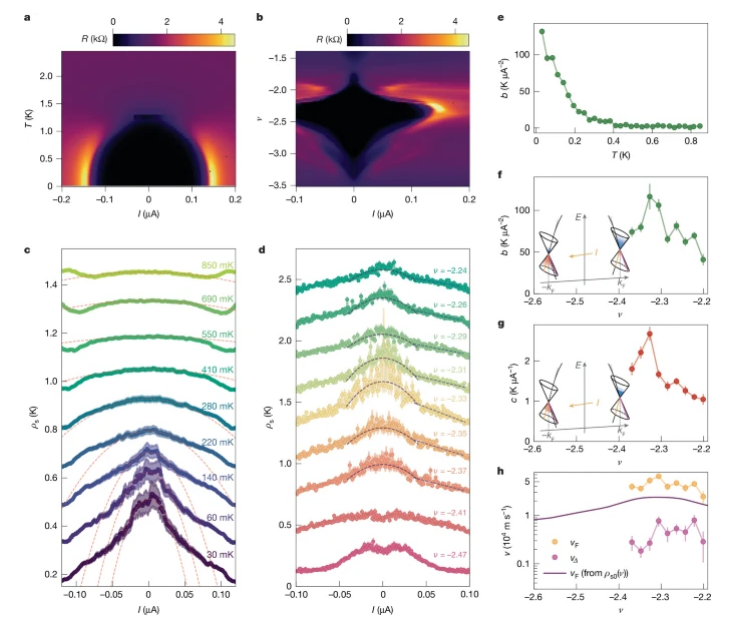
Fig 4. 非线性迈斯纳效应与节点超导特征a. 最佳掺杂点（ν = -2.34）附近直流电阻R随电流偏置I与温度T演化的二维相图，临界电流I_c≈0.12微安达最大值。b. 超流电阻R在电流偏置I与莫尔填充因子ν构成的参数空间中的响应规律。c. ν = -2.34处不同温度下测量的超流刚度ρ_s(I)曲线。零电流处曲率随温度升高逐渐衰减。d. 30 mK低温下，超流刚度ρ_s在ν = -2.24至ν = -2.47区间的电流依赖关系。最佳掺杂附近呈现显著的双模响应：低电流区（I→0）：ρ_s(I)∝−I², 高电流区（I < I_c≈0.12微安）：ρ_s(I)∝−I（曲线经垂直平移以增强区分度）e. 零电流处曲率参数b(T)的温度依赖性，其低温发散行为（T→0）是节点超导的强有力证据。
f-g. 曲率参数b (f) 与线性斜率c (g) 的基温测量值随ν演化规律。h. 基于ρ_s(I)与ρ_s(T)反演的费米速度参数：v_F≈ (0.1-0.7)×10⁵ m/s  v_Δ ≈ (0.2-0.5)×10⁴ m/s（实线为基于平滑化实验数据ρ_s0(ν)的理论预测值）插图：非线性迈斯纳效应两阶段机理示意图f插图：I→0时温度与电流共同激发准粒子g插图：I > I*时电流主导的准非平衡态分布。
 
        相关研究工作由哈佛大学Philip Kim/RTX BBN 技术公司Kin Chung Fong团队于2025年联合发表在《Nature》期刊上。Superfluid stiffness of twisted trilayer graphene superconductors，原文链接：https://doi.org/10.1038/s41586-024-08444-3

转自《石墨烯研究》公众号